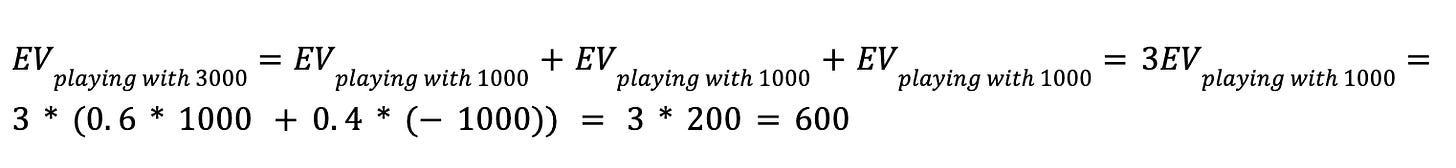Gambling vs. Risky Decisions
A quantitative frame of thought to distinguish between gambling and risky decisions
You may hear many dialogues like:” if you don’t gamble, you’ll never win” or “take the risk or lose the chance.” Usually, people use these quotes to justify decisions they’ve taken and may not be sure about the result. Results may have a big reward with little chance or high cost. But is it the true meaning of these statements? Are gambling and risky decisions the same?
In the investment industry, These statements may be heard more by growing highly volatile markets like high-tech stocks and cryptocurrencies and their derivatives like NFTs these days. Many investors make decisions and wait for big rewards while rationalizing their actions by saying, "we’ve taken some risks.” while in fact, they didn’t! They have gambled! Even some portfolio managers and experienced investors may have made the same mistake.
Note that here I don't want to argue whether risky decisions are good or bad or whether it is worth investing in risky markets or not. The mistake I wish to discuss is that we may gamble on something and think we have taken a risk. The important thing is distinguishing between gambling and making risky decisions. Here I want to discuss a frame of thought on how to differentiate them.
To understand the problem better, let's assume a betting game. Suppose you've been offered to play a game with two different scenarios.
Scenario 1:
There is a black box that contains 100 different cards with numbers 1 to 100. A card will be randomly drawn from the box. If the card is 100, you win 100 thousand dollars; if not, you lose 100.Scenario 2:
The same box exists. Again, a card will be randomly drawn, if the card is 100, you lose 100 thousand dollars, and if not, you win 100 dollars.
Which game would you play? Which game is risky, and which one is gambling? Here is where the math comes in and helps us. To answer these questions, we should calculate the expected value of winning. Based on the EV (Expected value) formula:
We should calculate the probability of outcomes and rewards (or punishments) associated with each one. In the mentioned game, we can easily calculate these parameters for both scenarios:
Thus, we can calculate EV:
The EV would determine if it is rational to play the game or not. If the EV is positive, it means it is worth taking the decision and playing the game, and if the EV is negative, it means it isn't worth it. Note that it doesn’t mean that you can achieve the EV by playing each scenario. It indicates whether playing the game is a rational decision or not.
There is a meaningful relationship between EV and the number of players playing a game. Consider that In the second scenario, despite the 99% probability of winning the game, playing is not rational due to its EV. Also, in the first game, the probability of a win is only 1%, but it is worth playing. Indeed, playing the first scenario is rational despite being too risky. However, if we play the second scenario, we are just gambling, even if the win probability is too high.
In "Thinking in bets," Annie Duke discusses improving the decision-making procedure. As she mentioned there, when you ask people to judge their decisions, they usually measure their decisions by the decision's results. It is a common trap that many people get stuck in. Their results can not assess the quality of their decisions. Many rational and intelligent choices didn’t result in desirable outcomes, while terrible decisions may have good results. Therefore a decision can not be assessed by its result. EV-based thinking is a valuable framework for evaluating a decision's quality. But it has some characteristics that should be noticed. Let's check other scenarios.
Zero EV
Assume the previous card game. We can change the rewards to generate the following scenarios:
These scenarios both have the same EV equal to zero. From the EV perspective, it doesn't matter which game you play. But are they the same? Both scenarios have the same EV; however, there is a significant difference in the probability of winning, so we should choose the game with a higher probability of winning.
Expected value linearity
Now consider scenario one and scenario 3. Their probabilities are the same and have the same amount of loss. The only differentiation is the reward of winning. In scenario 1, we have a positive EV (+901), while In the third scenario, we face a zero EV. In other words, the minimum reward of winning to have a non-negative EV (by fixing other parameters) is 9900. We will have a higher EV by growing the reward of winning up to 9900. To sum up, if the winning reward is greater than 9900, playing the game would be risky, while for any other reward setting, it would be gambling.
Now, let's scale the reward of scenarios 1 and 2 by 1000.
We are going to have the following:
The EV has also been scaled up to 1000. Still, scenario five is rational and risky, and scenario 6 is gambling.
EV blindness
Let’s consider the last example. Note that the game mechanics do not change, and the possibility of winning and losing while playing the scenarios remains the same, whereas EV has been growing 1000 times. Comparing scenarios 1 and 5, EV tells us that scenario 5 has a greater EV and is more attractive to play. But should we bet and play scenario 5? Is it 1000 times more rational than scenario 1? Assume someone with $100k total assets. Is it reasonable for him to bet all of his assets in scenario five because it has a 1000 times bigger EV than scenario 1? It does not make sense!
Here is where risk management comes into play. Indeed first, we should decide whether our game/investment/bet/decision is gambling or not. Is it rational to play or not? And then, we should use other tools to manage our risks. Kaley criteria, value at risk, and different methodologies have been introduced to manage the risk appropriately. Moreover, many concepts in behavioral finance argue that the numbers people read are not interpreted and are not understood the same. Therefore numerical risk modeling can not address the problem merely, and risk management needs to be addressed by behavioral finance concepts like risk profiling tools.
Expected value and the number of bets
As mentioned before, EV does not represent how much we will achieve through playing the game. It is a tool to express the boundary between a rational decision and gambling. But is there any relation between the EV and the actual reward? Let's assume a game with the following setup.
Suppose we want to participate in this game for $3000. Therefore our winning reward will be +3000, and our loss will be -3000. By setting up this configuration the EV is 0.6*3000 + 0.4*(-3000) = +600. So playing this game is rational. On the other hand, the outcome may be +3000 by 60% and -3000 by 40% chance.
Reducing the risk
Let's play this game with the same budget (3000) but divide it into three independent bets, each with 1000$. Due to Expected value linearity, the EV is:
The EV remains the same as before (600). But the outcomes changed to four different values with different possibilities. The following table shows the chances of the outcome.
The above table can indicate three main points:
The chance of winning the game has been increased to (0.432 + 0.216 =) 64.8%, despite the first setup where it was 60%
The first scenario outcomes still exist but with fewer probabilities:
Double up your money (+3000): 21.6% vs. 60%
Loos all of your money (-3000): 6.4% vs. 40%
the most probable outcome has been changed to +1000
Since I prefer simulations over theoretical mathematics, let’s see what happens if we simulate playing this game with a similar approach but divide it into 3000 (~∞) little games, each played for 1$. Here the result of 10000 times simulation is illustrated.
The result of simulations quickly demonstrates that by increasing the number of bets to 3000 (~∞), the probability of outcomes reforms to a gaussian distribution with mean = +600, equal to the original EV. Now let's rephrase the three main points again:
The chance of winning the game has converged to ~ 100 % despite the first setup, where it was 60%
The probabilities of the first outcomes (+3000 or -3000) both converge to ~ 0%
The most probable outcome has been changed to +600, the original EV.
In summary, We decided to play a game that is rational to play, and it has a risk to take. Indeed we take a risk to play the game, and then by dividing our initial assets into small ones and increasing the number of bets, we have reduced our risk. But in the real world, this method does not address the two remaining challenges. Namely:
Increasing the number of bets in many situations is impossible or very hard to do.
Many people wouldn’t be happy with the EV amount! Suppose the mentioned game, where the most probable outcome was 3000, and by increasing the number of bets, we reduced it to 600.
Therefore we need more information to analyze real cases.
Modifying risk
In the previous example, we saw two configurations for the same game. On the one hand, we had one bet, and on the other, we could play 3000 (~∞) times. Now let’s see what is happening between these numbers. To do this, let's change the number of bets from 1 to 1000 and see what will happen for the mean and the std of possible outcomes.
As expected, after increasing the number of bets, the most probable outcomes converged to EV.
Moreover, the outcomes' standard deviation (std) has also decreased significantly. Now let's zoom in on the initial iterations.
We can see that, in our game, the number of bets quickly affects convergence. In other words, in this game, we could play fewer iterations to achieve the EV amount with high confidence. If our minimum confidence level for winning the game is 95% (mean - 2*std), then we can play with ~ 96 bets instead of 3000 or 1000 (addressing the first challenge).
Some players may like to take more risks to achieve more gains. They can modify their risk by changing the number of bets to find a suitable trade-off point between their confidence levels and possible rewards. Here is where risk management and risk profiling cross over.
I've discussed how we should differentiate between taking risks and gambling. And how we can manage the risk in these kinds of decisions. As a quant researcher, I like to increase my confidence and model the problem numerically instead of deciding based on intuition. I hope this mechanism helps others to make informed decisions and avoid gambling. I’ve seen many Investors facing investment opportunities who made a mistake differentiating risk and gambling. Taking risks is a rational decision, but gambling is not. Besides, numerical and quantitative approaches increase confidence levels and reduce the risk we should take advantage of. The following flow chart may summarize what we have discussed: